摘要:利用一缓和曲线算例,通过数学分析,推导出缓和曲线逐桩坐标计算公式,此公式可作为道路测设中的范例来运用,有很强的指导意义。
关键词:缓和曲线、公式、逐桩坐标
一、 引言
道路建设中,由于受地形或地质影响,经常需要改变线路方向,为满足行车要求,往往要用曲线把两条直线连接起来。曲线的构成形式无外乎圆曲线和缓和曲线,本文以河北省沿海高速某曲线段为例推导出缓和曲线的逐桩坐标计算公式,以方便图纸的审核,满足施工放样的需求。本公式具有良好的操作性,方便施工、提高精度,可作为道路测设中的范例运用。
二、公式推导
1 、实例数据
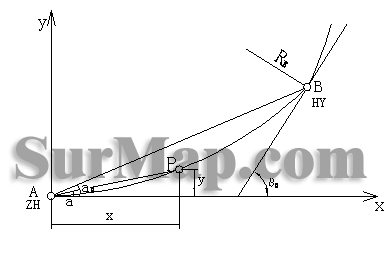
河北省沿海高速公路一缓和曲线(如图): AB 段为缓和曲线段, A 为 ZH 点, B 为 HY 点, RB=800m ; A 点里程为 NK0+080 ,切线方位角为 θA=100 ° 00 ′ 24.1 ″,坐标为 XA=4355189.493,YA=476976.267 ; B 点里程为 NK0+158.125 ,切线方位角为 θB=102 ° 48 ′ 15.6 ″,坐标为 XB=4355174.669 , YB=477052.964 ,推求此曲线段内任意点坐标。
2 、公式推导及实例计算
方法一:弦线偏角法
1 )公式推导
由坐标增量的计算方法我们不难理解,求一点坐标可以根据其所在直线的方位角以及直线上另一点的坐标和距待求点的距离。所以我们可以利用 ZH 点,只要知道待求点距 ZH 点的距离(弦长 S )和此弦与 ZH 点切线方位角的夹角(转角 a ),即可求出该点坐标。
根据回旋线方程 C=RL ,用 B 点数据推导出回旋线参数:
C=RLS=800*78.125=62500 ( LS 为 B 点至 ZH 点的距离)
设待求点距 ZH 点距离为 L
因回旋线上任意点的偏角 β0=L2/2RLS, 且转角 a=β0/3 ,
可得该点转角 a 。(曲线左转时 a 代负值)。
根据缓和曲线上的弧弦关系 S=L-L5/90R2LS2 ,
可以求出待求点至 ZH 点的弦长。
然后我们利用坐标增量计算公式可以推导出缓和曲线任意点坐标计算公式:
X=XA+S*cos ( θA+a ) =4355189.493+ ( L-L5/90R2LS2 ) *cos ( θA+L2/6RLS )
Y=YA+S*sin ( θA+a ) =476976.267+ ( L-L5/90R2LS2 ) * sin ( θA+L2/6RLS )
式中 θA=100 ° 0 ′ 24.1 ″
2 )实例计算
现在我们利用此公式计算桩号为 NK0+140 的坐标
第一步,求出 L=140-80=60 米
第二步,求出 a=180L2/6 π RLS=0 ° 33 ′ 00.14 ″
第三步,求出 S=L-L5/90R2LS2=60-605/ ( 90*8002*78.1252 ) =59.998
第四步:将 a , S 值代入缓和曲线计算公式,可求出桩号为 NK0+160 点的坐标为:
X=4355178.501 , Y=477035.249 。
同理,我们可求出其它桩号的坐标。
方法二:坐标转换法
1 )公式推导
首先我们建立坐标系,以 ZH 点为坐标原点,其切线方向为 X 轴,过该点的半径方向为 Y 轴(如图)。根据缓和曲线参数方程:
x=L-L5/40R2LS2 ;
y=L3/6RLS
计算出曲线上各点在此坐标系下的坐标( x , y )。
然后利用坐标转换公式
X=XA+xcosa-ysina
Y=YA+xsina+ycosa
将 (x,y) 代入该式,即可求出缓和曲线上各点的坐标计算公式:
X=4355189.493+ ( L-L5/40R2LS2 ) cosθA - ( L3/6RLS ) sinθA ;
Y=476976.267+ ( L-L5/40R2LS2 ) sinθA + ( L3/6RLS ) cosθA 。
式中 θA=100 ° 0 ′ 24.1 ″
2 )实例计算
现利用此公式计算桩号为 NK0+140 的坐标。
第一步:求出 L=140-80=60 米
第二步:求出该点在新坐标系下的坐标 x=59.995 ; y=0.576 。
第三步:将 L 、 x 、 y 的值代入公式可得 NK0+140 的坐标为:
X=4355178.501 , Y=477035.249 。
同理可计算出曲线上其他对应桩号的坐标:
NK0+100 : X=4355185.997 ; Y=476995.959 。
NK0+120 : X=4355182.375 ; Y=477015.628 。
为提高计算结果的准确性,提高工作效率和减轻计算的工作量,在实际应用中可以配合电子计算器使用,以下是 CASIO4800P 计算器计算缓和曲线的公式:
Lbl 0:{EG}:A “ X0 ” :B “ Y0 ” :C “ C0 ” :D “ 1/R1 ” :E “ 1/R2 ” :F “ DK1 ” :G “ DK2 ”
Lbl 1:{HOR}:H “ DKi”:O “ DL”:R”DR”:H>G => Goto 2 ◣
P= ( E-D ) /Abs(G-F):Q= Abs(H-F):I=P*Q
J=C+(I+2*D)*Q*90/ π◢
M=C+(I/4+2*D)*Q*45/2 π :N=C+(3*I/4+2*D)*Q*135/2/ π :K=C+(I/2+2*D)*Q*45/ π
X=A+Q*(cos C+4*( cos M + cos N)+2* cos K+ cos J)/12 ◢
Y=B+Q*(sinC+4*(sin M + sin N)+2* sin K+ sin J)/12 ◢
Goto 1 ◣
说明: A 为缓和曲线起点处的纵坐标( X 坐标);
B 为缓和曲线起点处的横坐标( Y 坐标);
C 为缓和曲线起点处的切线方位角;
D 为缓和曲线起点处的曲率半径;
E 为缓和曲线终点处的曲率半径;
F 为缓和曲线起点处的里程;
G 为缓和曲线终点处的里程;
H 为缓和曲线中所要放样点处的里程;
注意事项: D 和 E 值分别为该缓和曲线前后两段曲线元半径的倒数(即 1 / 半径),特别需要强调的是,当曲线右转的时候曲率半径输入时为正值,左转的时候输入时为负值, ZH 点的半径输“ 0 ”。
三、缓和曲线逐桩坐标计算公式应用
利用以上方法计算出对应桩号的坐标值,与图纸给出的数值相比较,看两者是否一致,以达到对图纸审核的目的。在施工过程中,利用此方法可以提高工作效率和精度,在设计图纸提供的点坐标不能满足实际要求时,可以计算出任意点的坐标值来解决实际问题,此计算方法在施工放样等道路测设中起到一定作用。
四、结语
在沿海高速公路的道路测设中运用此方法,提高了图纸复核的速度,对现场的施工放样和复核施工人员的测量资料都起到了一定的作用,通过实践验证了此方法在道路测设中有较强的实用价值,值得推广。
