论文导读:图2是为Lorenz教堂所建的FLAC3D模型。地基和隧道支护力学参数表3。在未来的地铁隧道施工中。用数值模拟的方法。数值模拟,城市地铁施工对浅表地基影响及防治措施的数值分析。
0 引言
浅埋暗挖法在北京地铁建设中成功应用以来,在上海、成都、广州、深圳、南京等地的地铁施工中都采用了此法,在未来的地铁隧道施工中,浅埋暗挖法具有非常广阔的发展前景。在地铁的建设中,人们最关心的是地铁隧道施工对城市环境的影响,即对已有临近城市地下管线、房屋基础及道路交通等的正常使用,因此,准确预测及现场的测量反馈施工引起的现场地层变形及其影响范围对施工安全和设计都是十分重要的[6]。
地铁隧道施工中对现场环境的检测可以指导地下工程施工,由此调整施工工艺和设计参数,反分析隧道结构受力和地层变化规律。以现有的工程的测量数据,对相似地质条件下的复杂工程进行对比参考设计,在重要路段,用数值模拟的方法,就地铁施工对地表已有城市建筑的影响进行预测,及时改变施工和设计方法,在现今的城市轨道交通的设计中有着非常实用的应用领域。此文以一具体地铁工程实例,用数值模拟方法对城市地铁隧道施工对浅地表高层建筑地基的影响及防治措施来进行分析,起到抛砖引玉的作用[6,7]。
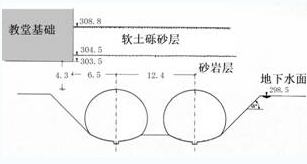
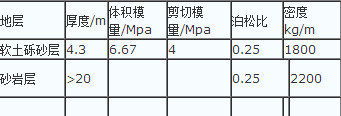
某市的地铁一号线横穿整个老城区,并且要在Lorenz教堂旁施工,Lorenz教堂历史悠久是某市的标志性建筑,所以对工程有着特殊的要求,不能因为地铁施工影响到教堂的结构安全。地铁由两个隧道组成,某市的地铁一号线横穿整个老城区,并且要在Lorenz教堂旁施工,Lorenz教堂历史悠久是某市的标志性建筑,所以对工程有着特殊的要求,不能因为地铁施工影响到教堂的结构安全。地铁由两个隧道组成,并且两隧道同时开挖,其空间布局和地质情况如图1所示,地下水位为地表以下10.3 m,隧道开挖所属的地层伴有沙层,施工难度很大,隧道附近的地层按照实地勘察和实验数据,大致分为两层,厚度及物理力学参数见表1。毕业论文,数值模拟。毕业论文,数值模拟。
隧道设计断面如图1所示,支护设计为混凝土C20与格栅钢架(主筋ø22)、锚索(R25/4外径/壁厚, L 长度 = 3.5 m, 间距 750 mm x 800 mm)的联合支护,总厚度达20 cm。图1 的左上表示的是Lorenz教堂的南地基,也是受隧道建设影响最大的地方,地基基础的埋深为-5.3 m。
2 确定计算参数,建模和计算
2.1 定义物理力学参数
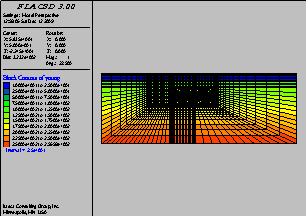
图2是为Lorenz教堂所建的FLAC3D模型。近地表的方块表示的是软土砾砂层,其下都表示为砂岩层,中间P2所指的块体表示的是Lorenz 教堂的两个地基,在砂岩地层中的两个半径为5m的圆形面积,表示的是待挖的隧道。P1、P2和P3分别表示来自教堂的不同建筑荷载,其具体数值和含义见表2。
图 2 Lorenz教堂在程序FLAC3D里的计算模型
荷载定义表2

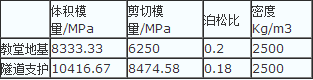
在FLAC 3D程序里,对Lorenz教堂的地基基础和隧道支护的物理力学特性将按照表3进行定义:
地基和隧道支护力学参数表3
将图3中的实验数据通过FLAC软件的程序语言输入软件中,经过计算得到了图4(杨氏模量在地层中的分布)的计算结果。由于软土砾砂层的成份分布复杂,按照[1]为了方便计算和定义软土砾砂层的弹性模量统一定义为10 MPa。
图 4 杨氏模量在地层中的分布
2.2 确定砂岩侧压系数K0
大部分的数值模拟软件都是将岩石的侧压系数K0以1来计算的(但是在浅地表的地层中,K0普遍都小于1,因为只有达到一定深度以后,各向受力的围岩将处于隐塑性状态。在这种状态下K0值才趋于1)或者通过其他半经验公式来确定,但是很多地质情况是比较复杂的,比如盆地和山谷,在这些地质情况下,侧压系数将大于1,如果地质情况是山脊,那么侧压系数将小于1,它不是一个材料常数,而是由地质的特点、地质运动和地形所影响的[3,5]。在实际情况中E=E(z); K0=K0(z)都是随深度变化而变化的参数,按照土力学理论K0=μ(z),式中μ为水平方向的泊松比。如[2]所述,经过实验得出浅表砂岩(地下5-25m)的泊松比为常数0.25,所以在本例中,将假设K0也为一常数。
为了更好地模拟Lorenz教堂地区的地层性质,需要找到合适的岩层的侧压系数K0,这就需选择在一个相似的地质条件下的隧道施工中,通过把实地测量的地表位移测量值与以不同侧压系数下数值模拟计算出来的计算值进行比较,找到一个合适的系数值。
σxx=σyy=K0σzz
式中σxx=σyy 是水平应力,σzz是竖直的应力,K0是侧压系数。毕业论文,数值模拟。
图 5 BW 210 平面图和地表沉降测量值[1]
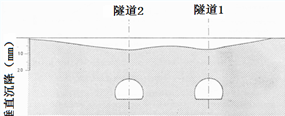
通过比较寻找,在某市地铁工程中,BW 210 段的工程地质条件很有代表性,与Lorenz教堂的地质情况非常相似,所以将BW210段工程作为比较计算地层。在图5中把I-I截面作为计算截面,图6是其计算截面在地铁施工后实地测量的沉降曲线。最大的沉降值以7.5和7.0 mm均出现在两隧道的正上方[4]。
图 6 I-I截面沉降曲线[1]
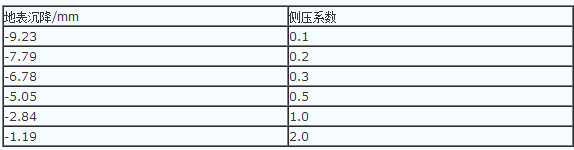
图7是通过FLAC 3D程序下进行的数值模拟,显示地表在不同侧压系数的下的位移分布。本次计算,为了寻找到合适的侧压系数K0,一共针对6个不同侧压系数K0(0.1、0.2、0.3、0.5、1.0和2.0)进行计算,表4所示的是其各自的计算结果(最大沉降值)。实际情况下测量,最大的地表沉降是7.0至7.5 mm,所以合理的侧压系数应在0.2至0.3之间,所以在接下来的计算中将以侧压系数0.25进行计算。图 6 I-I截面沉降曲线[1]
图7是通过FLAC 3D程序下进行的数值模拟,显示地表在不同侧压系数的下的位移分布。本次计算,为了寻找到合适的侧压系数K0,一共针对6个不同侧压系数K0(0.1、0.2、0.3、0.5、1.0和2.0)进行计算,表4所示的是其各自的计算结果(最大沉降值)。实际情况下测量,最大的地表沉降是7.0至7.5 mm,所以合理的侧压系数应在0.2至0.3之间,所以在接下来的计算中将以侧压系数0.25进行计算。
图 7 BW 210段在不同侧压系数条件下数值模拟地表沉降计算结果
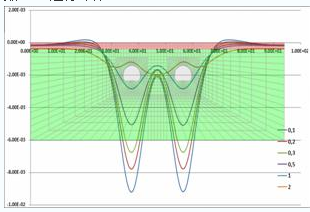
对应的侧压系数下地表最大沉降值表42.3 无防护措施时的高层建筑地基在地铁隧道暗挖施工地层的变形模拟分析
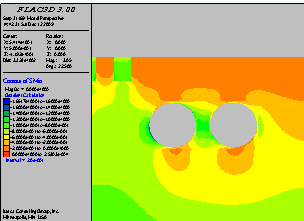
图8所示为隧道开挖后模型的最大应力分布,由于有教堂地基的荷载作用,应力分布在隧道周围不是对称的,最大压应力(数值为负,代表压应力)为-1.6517MPa出现在左隧道下半部。由于地基对上部荷载的传递作用,使得地基与周围土体的应力值有很大的区别。在两个隧道中间区域,也出现了压应力的跃升。
图 8 隧道开挖后模型的最大应力分布 [MPa]
隧道附近地层竖向位移(图9)在隧道开挖后也呈现出不对称的现象,最大的竖向位移发生在左隧道的拱顶部分(约-33mm),相对的最大的地层抬升发生在左隧道的底部(约15mm),与右边的隧道相比较,左隧道周围有变化较剧烈的应力分布和位移分布,这些都是由于左隧道与教堂的地基比较近,由教堂地基荷载的影响产生的。隧道开挖后,因为地层应力的重分布,以隧道中轴为限,隧道中心以下的地层都有略微的抬升,隧道中轴以上的地层都有不同程度的沉降,而且由图9看出,地层离隧道越接近,其竖向沉降值也越大。毕业论文,数值模拟。
图 9 竖直方向的位移 [m]
2.4防护措施的设计与数值模拟
对教堂地基的防护措施将主要以打混凝土支护桩外加预应力锚索的方式来进行加固,抵消由于地基荷载作用到隧道上所产生的应力。其设计示意图如图10所示,在隧道与教堂地基之间杨氏模量为30000MPa的混凝土支护桩,其设计半径及相隔距离见图11[4]。图12是在FLAC 3D里建的有安全措施的计算模型,预应力锚索按照表5的物理参数来进行计算[4]。毕业论文,数值模拟
图 10 附加安全措施(混凝土支护桩外加预应力锚索)的地铁计算截面
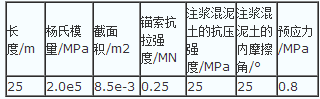
预应力锚索的力学参数表 5
图 12附加安全措施的计算模型
3 结论
通过计算,得出了最终的结果图13和14。计算得出的是地表水平和垂直位移变化,在没有安全措施情况下,两地基相对距离增加了约70mm (图14),右边地基左右两端的竖直沉降差达到了约5mm,这些都将导致拉应力在地基和建筑中的出现,降低了地基的承载能力,同时教堂的建筑危险性增加了。在有安全措施的情况下,在两个地基的位置上,发生的水平位移平均值是5mm,比没有安全措施时候模拟的要小约60%,而且地基附近的竖直沉降在与没有安全措施的相比较,减少了约80%。
从数值模拟的计算结果可知,隧道工程的施工在有安全措施:混泥土支护桩和预应力锚索的作用下,可以显著降低隧道工程的施工对Lorenz教堂地基的影响,有效的保护城市景观建筑的建筑安全。因此,在某市地铁Lorenz教堂段,相应的安全措施的建立是非常有必要的。毕业论文,数值模拟。
图 13比较有和没有安全措施情况下的地表沉降
图 14比较有和没有安全措施情况下的地表水平位移
本文通过FLAC 3D软件对地铁隧道施工的数值模拟,在具体施工前,对不同的施工方法分别进行数值模拟,计算结果比较分析,找到一个切实可行的施工方案,达到了保护著名建筑的目的。 FLAC 软件在对城市地铁隧道施工的数值分析方面,有着很好的应用前景。
参考文献
[1]Gartung E. Dubois J. Bauernfeind P.Stress and deformation calculation for the subway station Lorenz church in Nuremberg [G]. Eingenvertrag LGA Nürnberg, 1976: 15-45
[2]Hanke, H. Built in the Nuremberg areaon the example of the subway Nuremberg [G]. Eingenvertrag LGA Nürnberg. 1985: 12-18
[3]Duddeck, H. Gebel, H.P. Stress oftunnel crossings – model [M]. Bericht Nr. 72 -2 University of Braunschweig.1972: 78-85
[4]lu, K. Numerical investigation of astructural measure to reduce settlements and displacements of a foundationunder the control of an urban underground construction works with the computerprogram FLAC3D the example of Lorenz church in Nuremberg [D] Institut fürGeotechnik und Markscheidewesen. 2009: 72-95
[5]Dimitrios K. Geotechnical engineering andtunnel construction tunnel mechanics [M]. Institut für Geotechnik und Tunnelbau.1998: 41-55
[6]孙钧,刘洪洲.交叠隧道盾构法施工土体变形的三维数值模拟[J]. 同济大学学报2002, 30(4): 379–385.
[7]黄俊.地铁隧道浅埋暗挖施工工艺对地层变形的影响[G]. 见地下铁道文集[C]. 2003: 583–588
