结构设计的基本规定
一、结构的功能要求
结构在规定的设计基准期内和规定的条件下必须具有安全性、适用性和耐久性等三方面的功能。
二、结构极限状态的定义和分类
1.定义
整个结构或结构的一部分,超过某一特定状态就不能满足设计规定的某一功能要求,则此特定状态称为该功能的极限状态。
2.分类
结构的极限状态分为两类,即:
(l)承载能力极限状态:结构或结构构件达到最大承载力、或出现疲劳破坏、或不能继续承载变形的状态。
(2)正常使用极限状态:结构或结构构件达到正常使用或耐久性功能的某项规定的限值。
三、结构可靠度的基本概念
1.结构的功能函数:Z=R-S
式中S——外部作用在结构上产生的效应(内力和变形);
R——结构能承受内力和变形的能力。
2.极限状态方程:Z=R-S=0,(表示结构处于极限状态)
当Z=R-S>0时,则表示结构处于可靠状态;
当Z=R-S<0时,则表示结构处于失效状态。
3.结构可靠度概念
S和R均不是定值,而是随机变量,所以对上述状态要科学的衡量,只能用概率的方法。只要Z=R-S≥0的概率(即可靠概率或称可靠度)大到人们足以放心,就可认为设计的结构是安全可靠的。
4.几个重要的概念:
(1)作用效应S的不确定性主要是由下列因素引起的:
1)荷载(或作用)本身的变异性;
2)内力计算假定与结构实际受力情况间的差异。
(2)结构抗力R的不确定性主要是由下列因素引起的:
l)材料性能的不确定性;
2)结构构件几何参数的不确定性;
3)结构构件抗力R的计算模式的不确定性。
(3)结构的可靠性:结构在规定时间内、规定条件下能完成预定功能的能力。
(4)结构的可靠度:结构在规定时间内、规定条件下能完成预定功能的概率(或称可靠概率Pa:)。
(5)失效概率Pf:结构功能在规定时间内、规定条件下不能完成预定功能的概率(Pf)。(Ps+Pf=1)
(6)可靠指标β:结构功能函数Z的平均值与其标准差的比值(它与Pf,有一一对应的函数关系)。
(7)目标可靠指标[β]:作为结构设计依据的可靠指标称为目标可靠指标[β],亦称设计可靠指标。
现行《混凝土结构设计规范》(GB 50010-2002)是采用以概率理论为基础的极限状态设计法,以可靠指标度量结构构件的可靠度,采用分项系数的设计表达式进行设计的。
钢筋混凝土结构特点和材料的力学性能
一、钢筋混凝土结构特点
钢筋混凝土结构是由钢筋和混凝土两种性能不相同的材料组成的。混凝土具有较高的抗压强度,但抗拉强度却很低(仅为其抗压强度的1/8~1/16);而钢筋则具有较高的抗拉强度和抗压强度,我们把这两种材料组合在一起,将钢筋主要用于受拉,而混凝土主要用于受压,发挥材料各自的特长,成为目前应用最为广泛的钢筋混凝土结构。
1.钢筋与混凝土能很好地结合在一起共同工作的主要原因是:
(1)钢筋与混凝土之间存在着良好的粘结。
(2)钢筋与混凝土两者的温度线膨胀系数很接近。(钢筋约为1.2×10-5,混凝土约在1.0×10-5~1.5×10-5之间)
(3)钢筋受到混凝土的保护而不易生锈,具有很好的耐久性。
2.钢筋混凝土结构的主要优点是:
(l)合理发挥了钢筋和混凝土两种材料的力学特性,成为承载能力较高的结构。
(2)钢筋混凝土结构具有很好的耐火性、整体性、可模性。
(3)钢筋混凝土结构中,混凝土对钢筋有很好的防护性,与钢结构相比可省去很大的经常性维修费用。
(4)便于就地取材,造价降低。
3.钢筋混凝土的主要缺点为:
(1)自重较大;
(2)抗裂性能较差;
(3)隔热和隔声的性能不够理想。
上述主要缺点,正随着材料和结构的不断发展,在不断地得到改进(如轻骨料混凝土,高强混凝土和预应力混凝土的发展)。
二、混凝土强度
强度分为标准值和设计值。将强度标准值除以材料分项系数即为强度的设计值。
1.立方体抗压强度标准值(记为fcu,k)
按标准方法制作养护的边长为150mm的立方体试件,在28天龄期用标准试验方法测得的具有95%保证率的抗压强度。
混凝土强度等级按其fcu,k值确定,即fcu,k为××N/mm2的混凝土记为C××。
素混凝土结构的混凝土强度等级不应低于C15;钢筋混凝土强度等级不应低于C20;当采用强度等级400MPa及以上钢筋时,混凝土强度等级不宜低于C25;承受重复荷载的钢筋混凝土构件,混凝土强度等级不应低于C20。
预应力混凝土结构的混凝土强度等级不应低于C30,不宜低于C40。
2.轴心抗压强度标准值(记为fcx)
按标准方法制作养护的截面为150mm×150mm,高度为h(h一般为150 mm的3~4倍)的棱柱体,在28天龄期用标准试验方法测得的具有95%保证率的抗压强度。其设计值记为fc。
3.轴心抗拉强度标准值(记为ftk)
它是采用棱柱体试件直接轴向拉伸试验或立方体试件的劈裂试验来测定的。
混凝土的抗拉强度很低,远小于其抗压强度(一般只有其抗压强度的1/8~1/1 6)。其设计值记为ft。
三、混凝土变形
混凝土变形有两类,一类是受力变形;另一类为体积变形,它与受力无关,如混凝土在结硬过程中的收缩(或膨胀)等。
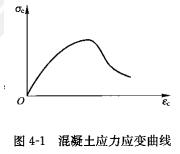
(一)混凝土的应力应变关系
混凝土在一次短期单轴加压时的应力应变关系如图4一1所示。是一曲线。所以其应力应变的比值(即σ/ε)是一个变量而不是常数,因此称E=σ/ε混凝土的变形模量。在计算设计时常用三种方式表示,即弹性模量Ec,变形模量和切线模量。
(二)混凝土的徐变
(1)定义:混凝土在恒定荷载的长期作用下,变形随时间而增长的现象称为徐变。
(2)影响徐变应变量(简称徐变)的因素有以下几方面:
1)水灰比大,水泥用量多,徐变量就大;
2)养护条件好,徐变量就小;
3)骨料质量及级配好,徐变量小;
4)构件体表比越大,徐变量越小;
5)构件的应力与其受荷时强度的比值(即σ/fc)越大,则徐变量越大。
(3)徐变对结构受力的影响:
1)徐变使结构的变形(包括挠度和裂缝)增大;
2)徐变使结构内部应力重分布;
3)徐变将引起预应力混凝土结构中的预应力损失;
4)受拉徐变,会延缓混凝土收缩裂缝的出现,及将减少由于支座不均匀沉降产生的应力等。
(三)混凝土的收缩(或膨胀)
(1)定义:混凝土在空气中结硬时体积缩小称为收缩,在水中结硬时体积膨胀称为膨胀;但收缩值要比膨胀值大得多。
(2)影响收缩值的因素有以下几方面:
1)水灰比大,水泥用量多,收缩值就大;
2)养护条件好,使用环境的湿度较高,收缩值小;
3)骨料质量及级配好,收缩值就小;
4)构件体表比越大,收缩值越小;
5)混凝土振捣密实,收缩值就小。
(3)收缩对结构受力的影响:
1)会在钢筋混凝土结构中,使混凝土产生拉应力,加速裂缝的出现和发展,甚至在未受荷前,即出现初始的收缩裂缝;
2)收缩将引起预应力混凝土结构中的预应力损失;
3)对跨度变化比较敏感的静定结构(如拱结构等)将产生不利的内力。
四、钢筋
1.混凝土结构中所用的钢筋主要可分为具有明显屈服点及屈服台阶的钢筋(或称软钢)和无明显屈服点及屈服台阶的钢筋(或称硬钢)两类。
2.现行的《混凝土结构设计规范》(GB 50010一2010)建议,纵向受力普通钢筋宜采用HRB400级、HRB500、HRBF400、HRBF500级钢筋,也可采用HPB300、HRB335、HRBF335、RRB400钢筋;梁、柱纵向受力钢筋应采用HRB400、HRB500、HRBF500钢筋,也可采用HRB335,HRBF335钢筋;预应力筋宜采用预应力钢丝、钢绞线和预应力螺纹钢筋。规范中对除HRB500,HRBF500级钢筋外的普通钢筋的受拉与受压强度设计值取相同。对预应力钢筋其受拉强度设计值远大于其受压强度设计值。
3.有时对软钢进行冷加工,提高钢筋的强度,以节约用钢。钢筋的冷加工有两种方式:即冷拉和冷拔。
冷拉后钢筋的抗拉强度提高,但其抗压强度未变(故其不宜用作受压钢筋),同时其屈服台阶缩短,伸长率减少,塑性降低,仍属软钢。
冷拔后钢筋的抗拉和抗压强度同时提高,但其已变为硬钢。
4.钢筋混凝土结构对钢筋性能的要求:
(1)钢筋应有较高的强度。对钢筋强度的要求主要有两个指标,即屈服强度和极限强度。屈服强度是设计计算时的主要依据。极限强度与屈服强度之比称为强屈比,强屈比越大,结构的可靠性越大。
(2)钢筋应有较好的塑性(或称延性)性能。它主要是用钢筋的伸长率和其冷弯性能来反映的。
(3)钢筋应与混凝土具有良好的粘结。
(4)钢筋还应具有可焊性。
五、钢筋与混凝土的粘结
1.钢筋与混凝土之间的粘结力主要是由三部分组成:
(1)化学胶着力;
(2)摩擦力;
(3)机械咬合力。
光面钢筋与混凝土之间的粘结力主要来自摩擦力,变形钢筋与混凝土之间的粘结力则主要来自机械咬合力,规范规定:对光面钢筋,其作受拉筋时,末端应做180°弯钩,弯后平直段不应小于3d;但其作受压时可不做弯钩。
2.影响粘结力大小的因素有以下几方面:
(1)钢筋的表面形状;
(2)混凝土强度等级;
(3)浇筑混凝土时钢筋所处的位置;
(4)保护层厚度和钢筋间的净距;
(5)横向钢筋(即箍筋)情况;
(6)侧向压力的作用。
承载能力极限状态计算
承受荷载产生的弯矩和剪力的构件,称为受弯构件(如梁、板)。它在弯矩作用下可能会发生正截面受弯破坏;同时在弯矩和剪力的共同作用下又可能会发生斜截面受剪破坏。
承受荷载产生的轴力、弯矩和剪力的构件,称为受压构件(即柱)。当然它也存在着正截面受弯破坏和斜截面受剪破坏的可能。
一、正截面承截能力计算
(一)破坏形态
(1)受弯构件(梁),因其配筋率ρ的不同,可能出现适筋梁破坏,超筋梁破坏和少筋梁破坏等三种。它们的破坏特征为;
1)适筋梁破坏(配筋量适中)——受拉区钢筋先达屈服强度,然后受压区边缘纤维混凝土的压应变达到其极限压应变。εcu值而破坏。该破坏属延性破坏。
2)超筋梁破坏(配筋量过多)——当受拉压钢筋还未达屈服强度,而受压区边缘纤维混凝土就因已达εcu值而破坏。该破坏属脆性破坏。
3)少筋梁破坏(配筋量过少)——当梁一开裂,受拉钢筋立即达屈服强度,梁被拉为两部分而断裂破坏。它的极限弯矩与开裂弯矩几乎相等,该破坏也属脆性破坏。
(2)偏压构件(柱)的破坏形态有:大偏心受压破坏和小偏心受压破坏等两种。它们的破坏特征为:
1)大偏心受压破坏——远离轴向力N一侧的受拉钢筋先达屈服强度,然后另一侧截面外边缘纤维混凝土的压应变达εcu而破坏。(时,该侧的受压钢筋也达受压屈服强度)。该破坏属延性破坏。
2)小偏心受压破坏——靠近轴向力N一侧的外边缘纤维混凝土压应变先达到εcu,同时这一侧的受压钢筋也达受压屈服强度;而远离轴向力N一侧的钢筋,无论是受拉还是受压,均未屈服而破坏。该破坏属脆性破坏。
(二)计算基本假定
(1)截面应变保持平面;
(2)不考虑混凝土的抗拉强度;
(3)混凝土受压的应力与应变关系曲线,如图4一3所示:

式中:σc——混凝土压应变为。。时的混凝土压应力;
fc——混凝土轴心抗压强度设计值;
ε0——混凝土压应力刚达fc时的混凝土压应变;
εcu——正截面的混凝土极限压应变,当处于非均匀受压时,按式(4一1)计算,当处于轴心受压时取为ε0。;
fcu,k——混凝土立方体抗压强度标准值;
n——系数。
(4)纵向钢筋的应力,取钢筋应变与其弹性模量的乘积,且此值应不大于其相应的强度设计值。纵向受拉钢筋的极限拉应变取为0.01。
(三)受压区混凝土的等效矩形应力图形
正截面破坏时受压区混凝土的应力图形可简化为等效的矩形,如图4一4所示。所谓等效,即为原应力图形的合力大小及其作用位置与矩形图形的合力大小及其位置相同。
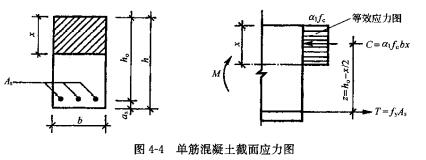
图4-4中系数αl的取值如下:
当混凝土强度等级≤C50时,αl=1.0
当混凝土强度等级>C80时,αl=0.94;
当混凝土强度等级在C50与C80之间时,则按线性内插法确定。
(四)相对界限受压区高度ξb
所谓界限破坏是指受拉钢筋受拉屈服与受压区混凝土外边缘纤维达εcu同时发生的破坏。所以其相对受压区高度ξb是判别适筋梁和超筋梁的界限条件。
按前述计算的基本假定可得ξb的计算公式为:

对常用钢筋可算得ξb值如下:
对HPB235级钢筋:ξb=0.614
对HRB335级钢筋:ξb=0.550
对HRB400级钢筋:ξb=0.518
